Gambar: Galena.co.id
A. Bentuk Pangkat
Bentuk pangkat meliputi: pangkat bulat positif, pangkat bulat negatif, dan pangkat nol.
Secara umum perpangkatan bulat positif suatu bilangan real didefinisikan:
B. Bentuk Akar
Pada bentuk akar berlaku:
C. Logaritma
Logaritma adalah Invers (kebalikan) dari perpangkatan, sehingga dapat didefinisikan sebagai berikut:
Keterangan:
a = Bilangan pokok atau basis logaritma.
x = Numerus, bilangan yang dicari logaritmanya, x > 0.
n = Hasil logaritma, nilainya dapat positif, nol, atau negatif.
A. Pengertian Relasi dan Fungsi
Relasi dari himpunan A ke himpunan B adalah pemasangan anggota-anggota himpunan A dengan anggota-anggota himpunan B. Sedangkan suatu Fungsi dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap anggota A dengan tepat satu anggota B.
Fungsi f dari himpunan A ke B ditulis:
(Dibaca: fungsi f memetakan A ke B)
B. Persamaan Kuadrat
Bentuk umum persamaan kuadrat:
Akar-akar persamaan kuadrat dapat ditentukan dengan:
- Memfaktorkan;
- Melengkapkan bentuk kuadrat sempurna;
- Menggunakan rumus abc:
Jumlah dan hasil kali akar-akar persamaan kuadrat:
1). Jumlah akar-akar persamaan kuadrat:
2). Hasil kali akar-akar persamaan kuadrat:
C. Fungsi Kuadrat
Bentuk umum fungsi kuadrat:
Cara-cara menentukan fungsi kuadrat:
A. Sistem Persamaan Linear
Sistem persamaan linear terdiri atas dua atau lebih persamaan linear. Sistem persamaan linear terbagi atas:
1). Sistem persamaan linear dengan dua variabel.
Bentuk umumnya:
a, b, c, p, q, r = bilangan real.
2). Sistem persamaan linear dengan tiga variabel.
Bentuk umumnya:
a, b, c, d, k, l, m, n, p, q, r, s = bilangan real.
3). Sistem persamaan linear dengan persamaan kuadrat.
Bentuk umunya:
;a, b, p, q, r = bilangan real.
4). Sistem persamaan kuadrat dengan dua variabel.
Bentuk umumnya:
;a, b, c, p, q, r = bilangan real.
B. Himpunan Penyelesaian Sistem Persamaan
Untuk mencari himpunan penyelesaian sistem persamaan linear dengan dua variabel dan persamaan kuadrat dapat dilakukan dengan beberapa cara, yaitu:
- Substitusi;
- Eliminasi; dan
- Gabungan substitusi dan eliminasi.
A. Pengertian Pertidaksamaan
Pertidaksamaan adalah suatu kalimat terbuka yang memuat satu variabel (peubah) atau lebih dan tanda-tanda ketidaksamaan.
B. Jenis-jenis Pertidaksamaan dan Penyelesaiannya
Berdasarkan pangkat dari variabelnya (bentuk pertidaksamaan), pertidaksamaan dapat dibagi atas:
1). Pertidaksamaan linear, adalah suatu pertidaksamaan yang mempunyai variabel pangkat satu.
Contoh: x + 4 < 2x + 7
2). Pertidaksamaan kuadrat, adalah suatu pertidaksamaan yang mempunyai variabel pangkat.
Contoh:
5).
Peluang komplemen suatu kejadian berlaku:
Frekuensi Harapan
Jika suatu percobaan dilakukan n kali maka peluang kejadian yang diharapkan adalah P(E). Perkalian antara berapa kali percobaan dilakukan dengan peluang kejadian itu dinamakan frekuensi harapan
Ditulis dengan:
n = banyak kejadian
Kejadian Majemuk
Pada kejadian majemuk berlaku:
Peluang kejadian saling asing atau kejadian saling lepas:
Untuk peluang kejadian sembarang A dan B berlaku:
Pada kejadian A dan B saling bebas, kejadian A tidak mempengaruhi kejadian B atau kejadian B tidak mempengaruhi kejadian A, sehingga berlaku:
Dua buah kejadian disebut kejadian tidak saling bebas, berlaku:
Peluang bersyarat P(B|A) artinya peluang terjadinya B setelah A terjadi.
A. Pengertian Relasi dan Fungsi
1. Produk Cartesius
2. Relasi
3. Fungsi
B. Sifat-sifat Fungsi
C. Aljabar Fungsi
Jika f dan g adalah dua fungsi yang diketahui, maka fungsi yang merupakan jumlah, selisih, hasil kali, dan hasil bagi kedua fungsi tersebut masing-masing sebagai berikut:
D. Komposisi Fungsi
3). Pertidaksamaan pecahan, adalah suatu pertidaksamaan yang mempunyai bentuk pecahan dan mengandung variabel x pada penyebutannya.
Contoh:
4). Pertidaksamaan nilai mutlak (harga mutlak), adalah suatu pertidaksamaan yang mempunyai tanda mutlak. Pada pertidaksamaan nilai mutlak berlaku:
|x| > 0 sama artinya -a < x < a.
|x| < 0 sama artinya x < -a atau x > a.
5). Pertidaksamaan bentuk akar, adalah pertidaksamaan yang variabelnya terletak di bawah tanda akar. Cara penyelesaiannya diawali dengan menguadratkan kedua ruas.
Contoh:
A. Kalimat Terbuka, Pernyataan, dan Negasinya
Kalimat terbuka adalah suatu kalimat yang memuat variabel, nilai kebenarannya belum dapat ditentukan, apakah bernilai benar atau salah.
Pernyataan adalah suatu kalimat yang dapat ditentukan nilai kebenarannya, yaitu benar atau salah, tetapi tidak dapat terjadi benar dan salah bersamaan.
Ingkaran pernyataan (negasi pernyataan) adalah kebalikan dari pernyataan. Jika pernyataan benar, ingkarannya salah, dan sebaliknya.
Contoh:
p = Bandung adalah ibu kota Provinsi Jawa Barat. (benar/B).
Ingkarannya:
p = Bandung bukan ibu kota Provinsi Jawa Barat. (salah/S).
p = Tidak benar bahwa Bandung adalah ibu kota Provinsi Jawa Barat. (salah/S).
Pernyataan Majemuk
Pernyataan majemuk adalah pernyataam yang terdiri dari dua pernyataan atau lebih dapat dihubungkan dengan kata hubung: ...dan...,... atau ... , jika ... maka..., dan ...jika dan hanya jika ... .
Contoh:
Hari ini mendung atau langit berwarna biru.
Jenis-jenis Kalimat Majemuk
Ada empat pernyataan majemuk, yaitu:
1). Konjungsi, adalah gabungan antara dua pernyataan dengan memakai kata hubung "dan", dinotasikan:
Abel kebenaran konjungsi:
2). Disjungsi, yaitu gabungan antara dua pernyataan dengan memakai kata hubung "atau", dinotasikan:
Tabel kebenaran disjungsi:
3). Implikasi, adalah gabungan antara dua pernyataan dengan memakai kata hubung "jika ...maka ...", dikonotasikan:
Tabel kebenaran implikasi:
4). Biimplikasi, dibentuk dari
Dikonotasikan:
Tabel kebenaran biimplikasi:
B. Ingkaran Pernyataan Majemuk
Ingkaran pernyataan majemuk terbagi atas:
1). Ingkaran dari konjungsi, berlaku:
2). Ingkaran dari disjungsi, berlaku:
3). Ingkaran dari implikasi, berlaku:
4). Ingkaran dari biimplikasi, berlaku:
C. Konvers, Invers, dan Kontraposisi
Dari implikasi
Dapat dibentuk implikasi baru, yaitu:
¤ Konvers:
¤ Invers:
¤ Kontraposisi:
D. Pernyataan Berkuantor dan Ingkarannya
Pernyataan berkuantor terdiri atas:
1). Pernyataan berkuantor universal, dinotasikan:
Ingkarannya:
2). Pernyataan berkuantor eksistensial, dinotasikan:
Ingkarannya:
E. Penarikan Kesimpulan
Penarikan kesimpulan terbagi atas:
1). Penarikan kesimpulan dari pernyataan majemuk, dengan aturan:
a). Modus Ponens, berlaku:
b). Aturan Tollens, berlaku:
c). Silogisme, berlaku:
2). Penarikan kesimpulan dari pernyataan berkuantor.
Contoh:
p(x) : Jika suatu segitiga merupakan segitiga sama kaki maka mempunyai dua sudut sama besar.
=_ Setiap segitiga sama kaki mempunyai dua sudut sama besar.
A. Perbandingan Trigonometri
Rumus-rumus perbandingan trigonometri:
1).
2).
Perbandingan trigonometri sudut
dengan
3).
Perbandingan trigonometri sudut
dengan
4).
Perbandingan trigonometri sudut
dengan5).
B. Fungsi Trigonometri
Fungsi trigonometri dapat berbentuk sebagai berikut:
1).
2).
3).
C. Identitas Trigonometri
Contoh identitas trigonometri:
D. Persamaan Trigonometri
Untuk
(B = himpunan bilangan bulat), diperoleh persamaan sebagai berikut:
E. Aturan Sinus, Atuturan Kosinus, dan Rumus Segitiga
Aturan sinus:
A. Kedudukan Titik, Garis, dan Bilangan pada Bangun Ruang
Kedudukan titik dibedakan atas:
- Titik terletak pada garis.
- Titik terletak di luar garis.
- Titik terletak pada bidang.
- Titik terletak di luar bidang.
Kedudukan suatu garis terhadap garis lain (dua garis) dibedakan atas:
- Berimpit.
- Sejajar.
- Berpotong.
- Bersilangan.
Kedudukan suatu bidang terhadap bidang lain (dua bidang) dibedakan atas:
B. Proyeksi Ruang
Proyeksi ruang meliputi:
A. Statistika
Perbedaan Pengertian Statisik dengan Statistika
Statistik adalah kunmpulan angka-angka dari suatu permasalahan, sehingga dapat memberikan gambaran mengenai masalah tersebut. Sedangkan Statistika adalah cara ilmiah yang mempelajari pengumpulan, pengaturan, perhitungan, penggambaran, dan penganalisisan data, serta penarikan kesimpulan yang valid berdasarkan penganalisisan yang dilakukan, dan pembuatan kesimpulan yang rasional.
Penyajian Data Tunggal
Penyajian data dapat berupa:
Perbedaan Pengertian Statisik dengan Statistika
Statistik adalah kunmpulan angka-angka dari suatu permasalahan, sehingga dapat memberikan gambaran mengenai masalah tersebut. Sedangkan Statistika adalah cara ilmiah yang mempelajari pengumpulan, pengaturan, perhitungan, penggambaran, dan penganalisisan data, serta penarikan kesimpulan yang valid berdasarkan penganalisisan yang dilakukan, dan pembuatan kesimpulan yang rasional.
Penyajian Data Tunggal
Penyajian data dapat berupa:
- Diagram Batang, adalah penyajian data dengan menggunakan batang-batang berbentuk persegi panjang dengan lebar batang yang sama dan dilengkapi dengan skala tertentu untuk menyatakan banyaknya tiap jenis data.
- Diagram Lingkaran, adalah penyajian data statistik dengan menggunakan gambar yang berbentuk lingkaran, yang dibagi atas juring-juring.
- Diagram Garis, adalah penyajian data pada bidang Cartesius dengan menghubungkan titik-titik data pada bidang Cartesius (sumbu x dan sumbu y), sehingga diperoleh suatu grafik berupa garis.
- Diagram Batang Daun, adalah penyajian data yang dibagi atas dua bagian, yaitu bagian batang dan daun. Bagian batang memuat angka puluhan, sedangkan bagian daun memuat angka satuan.
- Diagram Kotak Garis, adalah penyajian data dalam bentuk kotak garis.
Penyajian Data Berkelompok
Apabila data cukup banyak maka data dikelompokkan dalam beberapa kelompok, kemudian data tersebut disajikan dalam bentuk tabel distribusi frekuensi.
Langkah-langkah membuat tabel distribusi frekuensi adalah sebagai berikut:
1). Urutkan data dari data terkecil ke data terbesar.
2). Tentukan banyak kelas pada tabel distribusi frekuensi, dengan menggunakan metode Sturges:
Keterangan:
k = banyak kelas
n = banyak data
3). Tentukan interval kelas dengan rumus:
Keterangan:
l = interval kelas
R = range = jangkauan = data tertinggi - data terendah
k = banyak kelas
4). Tentukan batas atas kelas (Ba) dan batas bawah kelas (Bb).
Tabel distribusi frekuensi dapat dibedakan atas:
a). Tabel Distribusi Frekuensi Relatif: mempunyai frekuensi relatif dalam bentuk persentase (%). Besarnya frekuensi relatif dapat ditentukan dengan rumus:
Fungsi relatif kelas ke-k =
b). Tabel Distribusi Frekuensi Kumulatif, adalah tabel frekuensi yang berisikan frekuensi kumulatif (frekuensi hasil akumulasi). Frekuensi kumulatif adalah frekuensi yang dijumlahkan, yaitu frekuensi suatu kelas dijumlahkan dengan frekuensi kelas sebelumnya.
Ukuran Data Statistik
a). Ukuran Pemusatan Data (Ukuran Tendensi Sentral)
Ada tiga macam ukuran tendensi sentral, yaitu:
☆ Rata-rata atau mean
Yaitu jumlah seluruh nilai-nilai data dibagi dengan banyaknya data.
¤ Rata-rata untuk data tunggal (tidak berkelompok), rumusnya:
¤ Rata-rata untuk data berkelompok, rumusnya:
¤ Rata-rata sesungguhnya dengan memfaktorkan interval kelasnya, rumusnya:
¤ Rata-rata sesungguhnya dengan memfaktorkan interval kelasnya, rumusnya:
☆ Median (Md), adalah nilai yang terletak di tengah deretan data setelah diurutkan dari yang terkecil.
Rumus median untuk data berkelompok:
Keterangan:
Md = Median
Tb = Tepi bawah kelas
fk = frekuensi kumulatif
☆ Modus (Mo), adalah data yang paling sering muncul atau yang mempunyai frekuensi terbanyak.
Rumus modus data kelompok adalah:
b). Ukuran Letak
Ukuran letak suatu data dapat dinyatakan dalam bentuk fraktil.
Fraktil adalah nilai-nilai yang membagi seperangkat data yang telah berurutan menjadi beberapa bagian yang sama, yaitu:
☆ Kuartil, adalah ukuran letak yang membagi sekumpulan data tersebut menjadi 4 bagian yang sama.
Kuartil terbagi atas:
Rumus kuartil untuk data berkelompok:
☆ Desil, adalah ukuran letak yang membagi sekumpulan data menjadi 10 bagian.
Rumus desil untuk data berkelompok:
☆ Persentil, adalah ukuran letak yang membagi sekumpulan data menjadi 100 bagian.
Rumus kuartil untuk data berkelompok:
c). Ukuran Penyebaran Data (Dispersi)
Ukuran penyebaran data terbagi atas:
¤ Jangkauan atau range (R), berlaku:
¤ Simpangan rata-rata atau deviasi rata-rata (SR), rumusnya:
¤ Simpangan baku/standar deviasi/deviasi standar (SD), rumusnya:
¤ Simpangan kuartil atau jangkauan semi inter kuartil
Rumusnya:
B. Peluang
Permutasi
Permutasi adalah urutan yang mungkin dari sejumlah unsur yang berbeda tanpa adanya pengulangan.
Rumusnya:
Atau
Di mana
Permutasi terbagi atas:
1). Permutasi dengan beberapa objek sama, berlaku:
a). Banyaknya permutasi dari n objek dengan r objek sama(r < n) adalah:
b). Banyaknya permutasi dari n objek, di mana ada beberapa objek sama, misalnya ada
objek yang sama, ada
objek yang sama serta
objek yang sama, dan seterusnya adalah:
2). Permutasi Siklis, berlaku:
Banyaknya permutasi siklis dari n objek = (n - 1)!
Kombinasi
Banyaknya kombinasi r objek dari n objek ditulis dengan
Atau
Adalah
Peluang Suatu Kejadian
Peluang (P) merupakan ukuran mengenai kemungkinan suatu kejadian tertentu akan terjadi dalam suatu percobaan. Jika hasil suatu percobaan yang mungkin itu dihimpun dalam suatu himpunan maka himpunan itu disebut ruang sampel yang dilambangkan dengan S.
Peluang P untuk terjadinya suatu kejadian E adalah:
Keterangan:
P (E) = Peluang kejadian yang diharapkan sukses.
n (E) = Banyaknya anggota kejadian E.
n (S) = Banyaknya anggota ruang sampel (banyaknya kejadian yang mungkin terjadi).
Frekuensi Harapan
Jika suatu percobaan dilakukan n kali maka peluang kejadian yang diharapkan adalah P(E). Perkalian antara berapa kali percobaan dilakukan dengan peluang kejadian itu dinamakan frekuensi harapan
Ditulis dengan:
n = banyak kejadian
Kejadian Majemuk
Pada kejadian majemuk berlaku:
Peluang kejadian saling asing atau kejadian saling lepas:
Untuk peluang kejadian sembarang A dan B berlaku:
Pada kejadian A dan B saling bebas, kejadian A tidak mempengaruhi kejadian B atau kejadian B tidak mempengaruhi kejadian A, sehingga berlaku:
Dua buah kejadian disebut kejadian tidak saling bebas, berlaku:
Peluang bersyarat P(B|A) artinya peluang terjadinya B setelah A terjadi.
A. Pengertian Relasi dan Fungsi
1. Produk Cartesius
2. Relasi
3. Fungsi
B. Sifat-sifat Fungsi
C. Aljabar Fungsi
Jika f dan g adalah dua fungsi yang diketahui, maka fungsi yang merupakan jumlah, selisih, hasil kali, dan hasil bagi kedua fungsi tersebut masing-masing sebagai berikut:
D. Komposisi Fungsi
E. Fungsi Invers
F. Hubungan Komposisi dan Invers
G. Rumus-rumus
A. Pengertian Limit
B. Teorema Limit
C. Limit Fungsi Aljabar
A. Integral Tak Tentu
B. Sifat-sifat Integral
C. Penerapan Integral Tentu
D. Integral Tertentu
E. Sifat-sifat Integral Tertentu
F. Luas Bidang Datar
1. Dibatasi oleh Kurva dan Sumbu X
2. Luas antara Dua Kurva
G. Volume Benda Putar
1. Mengelilingi Sumbu X
2. Mengelilingi Sumbu Y
H. Integral Fungsi Trigonometri
I. Integral Substitusi Trigonometri
J. Panjang Busur
A. Persamaan Garis Lurus
B. Himpunan Penyelesaian dari pertidaksamaan Linear
C. Fungsi Tujuan (Objektif/Sasaran), Nilai Maksimum, dan Nilai Minimum
- Fungsi Tujuan adalah nilai f untuk x dan y tertentu dari suatu program linear, dan dinyatakan f (x,y).
- Nilai Fungsi Sasaran yang Dikehendaki adalah kondisi x dan y yang menyebabkan maksimum atau minimum.
- Pada gambar HP Program Linear, titik-titik sudut merupakan titik-titik kritis, dimana nilai minimum atau maksimum berada. Apabila sistem pertidaksamaannya terdiri dari dua pertidaksamaan, maka titik-titik kritisnya bisa ditentukan tanpa harus digambar garfiknya.
Berdasarkan kedua grafik di atas dapat disimpulkan cara penentuan titik kritis sebagai berikut:
- Pilih titik potong kurva dengan sumbu Y atau sumbu X yang terkecil (0, a) dan (q, 0) jika tujuannya maksimumkan atau yang terbesar (0, p), (b, 0) jika tujuannya minimumkan.
- Titik potong antara kedua kurva (x,y).
1. Pengertian Matriks
- Matriks adalah susunan kumpulan bilangan dalam bentuk persegi atau persegi panjang yang diatur menurut baris dan kolom;
- Baris suatu Matriks adalah susunan bilangan-bilangan yang mendatar dalam matriks;
- Kolom suatu Matriks adalah susunan bilangan-bilangan yang tegak dalam matriks.
2. Operasi Hitung Matriks
a). Penjumlahan atau Pengurangan Matriks.
Matriks A dan B dapat dijumlahkan atau dikurangkan jika ordo A = ordo B.
1). Sifat penjumlahan matriks
Jika A, B, dan C matriks-matriks berordo sama, maka berlaku:
- Sifat Komutatif: A + B = B + A;
- Sifat Asosiatif: (A + B) + C = A + (B + C);
- Terdapat matriks Identitas, yaitu matriks nol, sehingga: A + 0 = 0 + A = A;
- Setiap matriks A mempunyai invers penjumlahan yaitu matriks - A, sehingga: A + (-A) = (-A) + A = 0.
2). Pada pengurangan matriks bersifat:
- Tidak Komutatif;
- Tidak Asosiatif;
- Tidak terdapat unsur Identitas.
b). Perkalian Matriks
Dua matriks A dan B dapat dikalikan bila banyak kolom matriks pertama (kiri) sama dengan banyak baris matriks kedua (kanan).
3. Tranpos Matriks
4. Determinan dan Invers Matriks
5. Penggunaan Matriks dalam Sistem Persamaan Linear
1. Barisan dan Deret Aritmatika
2. Barisan dan Deret Geometri
3. Deret Geometri Tak Terhingga
Sumber: Ebook/http://pak-anang.blogspot.com
Editor: SowongFana







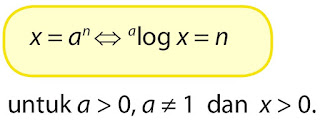
















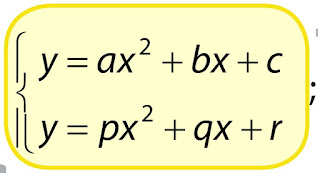




































































































































































































As claimed by Stanford Medical, It's really the one and ONLY reason women in this country live 10 years longer and weigh on average 19 kilos less than us.
BalasHapus(And really, it has NOTHING to do with genetics or some secret-exercise and really, EVERYTHING about "HOW" they are eating.)
P.S, I said "HOW", not "what"...
Click this link to uncover if this little quiz can help you discover your true weight loss potential